定义
关于背包的定义以及算法,网上有很多教程和解法,下图比较完整的介绍了几种常见的背包:
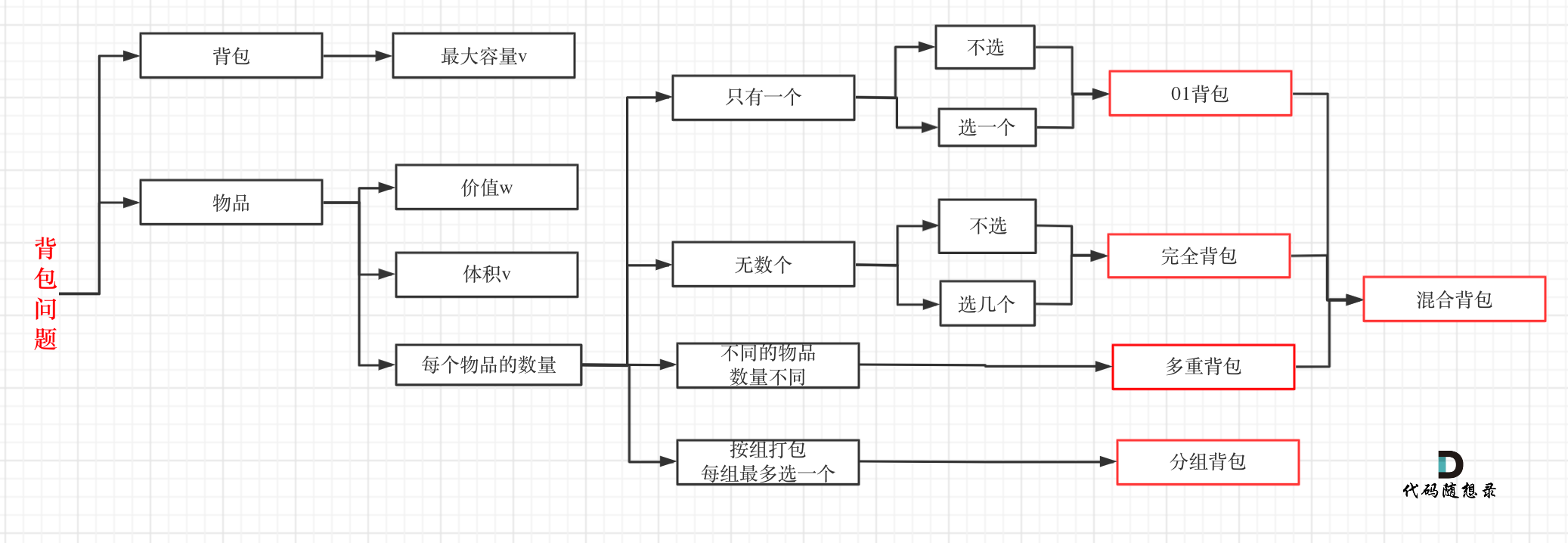
01背包
有n件物品和一个最多能背重量为w的背包。第i件物品的重量是w[i],得到的价值是v[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
比如有如下3个物品,背包的最大重量是4。如何安排能使背包的价值最大呢?
| 重量 | 价值 | |
|---|---|---|
| 物品1 | 1 | 15 |
| 物品2 | 3 | 20 |
| 物品3 | 4 | 30 |
暴力解法
如果不考虑时间复杂度,最先想到的其实就是暴力解法。
// 示例用法
var values = [15, 20, 30]; // 物品的价值
var weights = [1, 3, 4]; // 物品的重量
var capacity = 4; // 背包的容量
var result = bruteForce01Knapsack(values, weights, capacity);
console.log("最大总价值:", result[0]);
console.log("最优解决方案:", result[1]);
function bruteForce01Knapsack(values, weights, capacity) {
let n = values.length
let maxValue = 0
let bestSolution = []
// 遍历所有可能的解决方案(每个物品都可以放入或者不放入)
for (let i = 0; i < Math.pow(2,n); i ++) {
let solution = []
let totalValue = 0
let totalWeight = 0
// 将整数转换为二进制,并判断是否放入背包
for (var j = 0; j < n; j++) {
if ((i >> j) & 1) { // 获取二进制表示中第j位的值
solution.push(1); // 放入背包
totalValue += values[j];
totalWeight += weights[j];
} else {
solution.push(0); // 不放入背包
}
}
if (totalWeight <= capacity && totalValue > maxValue) {
maxValue = totalValue
bestSolution = solution
}
}
return [maxValue, bestSolution]
}
因为每个物品都可以放或者不放,所以可以用二进制来表示这n个物品的放入情况。
总共有 2^n 种组合方式,然后在每种方式里查看每个位置的情况,如果是1就加入背包,如果是0就不放入背包,最后算总重量和总价值是否满足情况。
上述暴力解法的时间复杂度为 O(2^n),随着物品数量的增加O也指数级增加,显然无法为我们解决比较复杂的01背包问题。
二维dp数组(动规五步法)
1. 确定dp数组以及下标意义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。 只看这个二维数组的定义,大家一定会有点懵,看下面这个图:
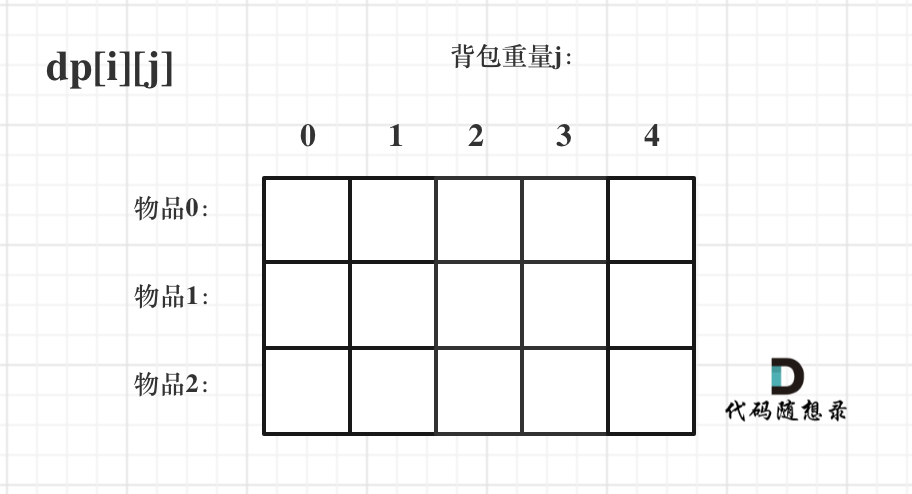
2. 确定递推公式
可以有两个方向推出来dp[i][j]。
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
在看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
3. db数组初始化
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
上述初始化的js代码如下:
// 背包重量比物品0的重量都要小
for (let j = 0 ; j < weight[0]; j++) {
dp[0][j] = 0;
}
// 背包重量大于物品0的重量
for (let j = weight[0]; j <= bagWeight; j++) {
dp[0][j] = value[0];
}
这时候的dp数组的初始化情况如下:
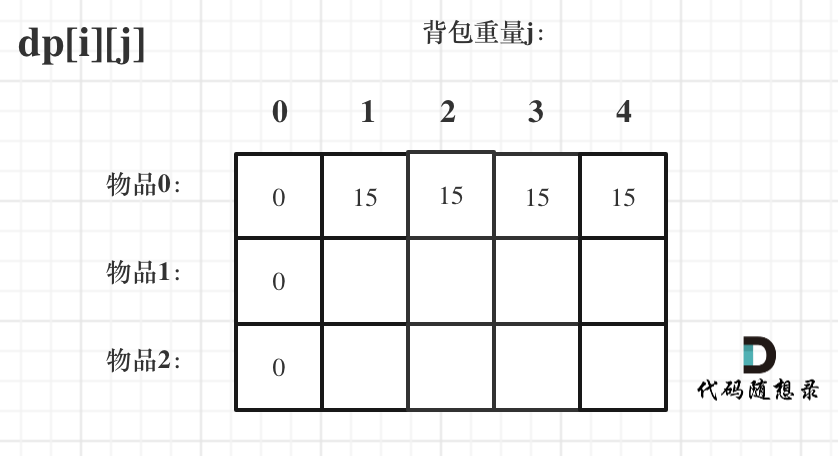
至于为什么先先做初始化,其实上述推断表达式也有表达,因为表达式依赖于 i-1,所以必须要把 dp[0][j] 的情况全部列出,以及 j为0的情况全部列出。
那么表格里面的其他未初始化的呢,其实可以初始化为0,因为在后面公式计算的时候都会重新赋值为正确的值,可以先用0填充。
4. db数组遍历顺序
这种写法先遍历物品还是先遍历背包重量都可以。为什么呢?
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程无非就是先按照行遍历还是先按照列进行遍历,结果都是遍历完整个左上角方向的块。
5. 举例演示dp数组:(手动计算和代码验证)
完整代码如下:
var values = [15, 20, 30]; // 物品的价值
var weights = [1, 3, 4]; // 物品的重量
var capacity = 4; // 背包的容量
function bagProblem(values, weights, capacity) {
// 定义db二维数组
const len = weights.length,
dp = Array(len).fill().map(() => Array(capacity + 1).fill(0));
// 初始化
for (let j = weights[0]; j <= capacity; j ++ ) {
dp[0][j] = values[0]
}
// weight 数组的长度len 就是物品个数
for (let i = 1; i < len; i ++)
for (let j = 0; j <= capacity; j ++) {
if (j < weights[i]) dp[i][j] = dp[i-1][j]
else dp[i][j] = Math.max(dp[i-1][j-weights[i]] + values[i], dp[i-1][j])
}
console.log(dp)
var max_value = dp[len -1][capacity];
// 构造最优解的物品选择方案
let best_solution = [];
let w = capacity;
for (var i = len -1; i >= 0 && max_value > 0; i--) {
if (i == 0) {
if (dp[i][w] === max_value) {
best_solution.push(i);
}
} else {
if (dp[i][w] !== dp[i - 1][w]) {
best_solution.push(i);
max_value -= values[i];
w -= weights[i];
}
}
}
console.log('best_solution', best_solution)
return max_value
}
console.log(bagProblem(values, weights, capacity))
一维dp数组(滚动数组优化)
滚动数组(Rolling Array)是一种优化技巧,用于减少动态规划中二维数组的空间使用。它适用于那些只需要保存当前状态和前一个状态的动态规划问题。
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
可以看出左右等式都和i有关,优化后变成了:dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
还是用动规五部曲分析如下:
1. 确定dp数组以及下标意义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2. 确定递推公式
上面其实已经推断出dp[j]的递推公式了。dp[j] = max(dp[j], dp[j - weight[i]] + value[i])。
其实dp[j]同样也是有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i。一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的。
3. db数组初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
4. db数组遍历顺序
for (let i = 1; i <= len; i ++)
for (let j = capacity; j >= weights[i-1]; j --) {
dp[j] = Math.max(dp[j],dp[j-weights[i-1]]+values[i-1])
}
这里和二维dp的写法中,遍历背包的顺序是不一样的!
为什么遍历背包容量的时候要倒序遍历。其实这是在做滚动数组优化的时候必要的,必须得这样。
因为如果一旦正序遍历了,那么物品0就会被重复加入多次!
比如:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] // 15
dp[2] = dp[2 - weight[0]] + value[0] // 30
如果倒序遍历
dp[2] = dp[2 - weight[0]] + value[0] // 15
dp[1] = dp[1 - weight[0]] + value[0] // 15
那如果改变两个嵌套for循环的顺序呢,答案是更不行了。 因为如果先遍历背包容量,再遍历背包,会导致每个容量只会放入一个物品了。
5. 举例演示dp数组:(手动计算和代码验证)
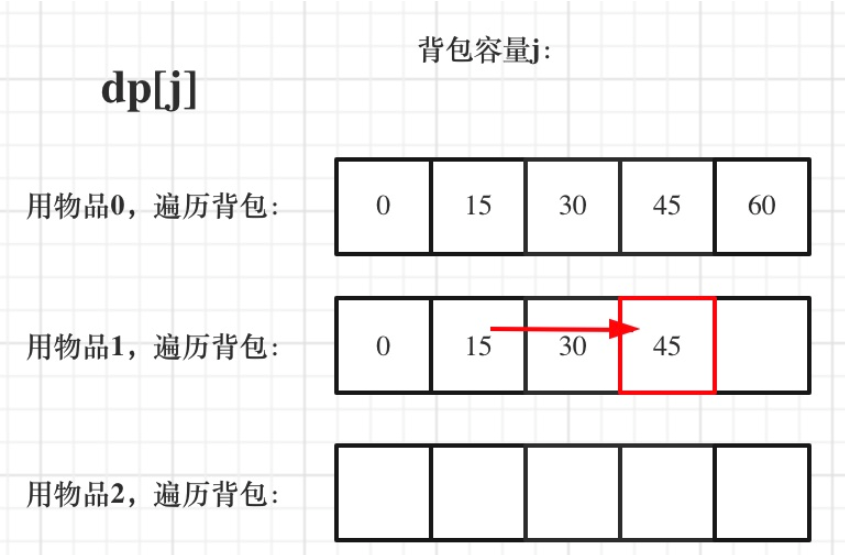
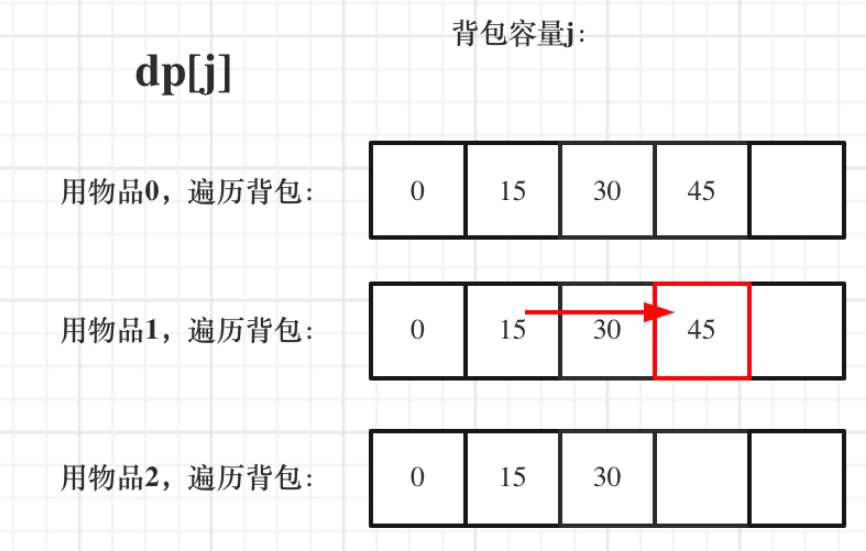
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
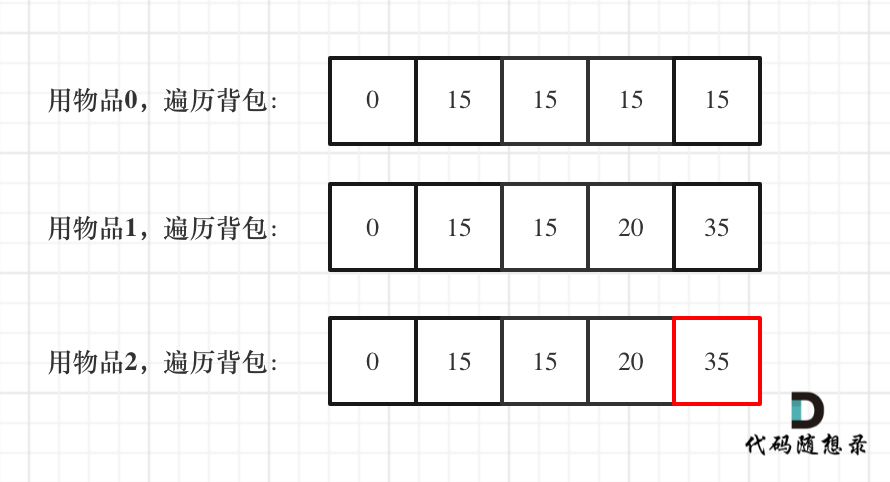
完整代码如下:
var values = [15, 20, 30]; // 物品的价值
var weights = [1, 3, 4]; // 物品的重量
var capacity = 4; // 背包的容量
// 滚动数组优化方案
function bagProblemFeature(values, weights, capacity) {
const len = weights.length,
dp = Array(capacity + 1).fill(0);
// weight 数组的长度len 就是物品个数
for (let i = 1; i <= len; i ++)
for (let j = capacity; j >= weights[i-1]; j --) {
dp[j] = Math.max(dp[j],dp[j-weights[i-1]]+values[i-1])
}
// for (let j = capacity; j >= weights[i-1]; j --) {
// for (let i = 1; i <= len; i ++)
// dp[j] = Math.max(dp[j],dp[j-weights[i-1]]+values[i-1])
// }
return dp[capacity]
}
console.log(bagProblemFeature(values, weights, capacity))
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
还是上面那个例子:
比如有如下3个物品,背包的最大重量是4。如何安排能使背包的价值最大呢?
| 重量 | 价值 | |
|---|---|---|
| 物品1 | 1 | 15 |
| 物品2 | 3 | 20 |
| 物品3 | 4 | 30 |
我们知道01背包内嵌的循环是从大到小遍历,是为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for (let i = 1; i <= len; i ++)
for (let j = weights[i]; j <= capacity; j ++) {
dp[j] = Math.max(dp[j],dp[j-weights[i-1]]+values[i-1])
}
那么完全背包的先后遍历顺序可以更换么,答案是可以的。
// 先遍历背包,再遍历物品
for (let j = 0; j <= capacity; j ++)
for (let i = 1; i <= len; i ++) {
if (j >= weights[i-1]) {
dp[j] = Math.max(dp[j],dp[j-weights[i-1]]+values[i-1])
}
}
真题
给定一个非负整数数组,a1, a2, …, an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
输入:nums: [1, 1, 1, 1, 1], S: 3 输出:5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
可以用01背包算法解决上述问题。假设加法的总和为x,那么减法对应的总和就是sum - x。所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,装满容量为x的背包,有几种方法。
动态规划5部曲:
- 确定db数组以及下标的意义:
dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
- 递推公式